An Improved Proof of the Handshaking Lemma
In 2009, I posted a calculational proof of the handshaking lemma, a well-known elementary result on undirected graphs. I was very pleased about my proof because the amount of guessing involved was very small (especially when compared with conventional proofs). However, one of the steps was too complicated and I did not know how to improve it.
In June, Jeremy Weissmann read my proof and he proposed a different development. His argument was well structured, but it wasn’t as goal-oriented as I’d hoped for. Gladly, after a brief discussion, we realised that we were missing a great opportunity to use the trading rule (details below)!
I was so pleased with the final outcome that I decided to record and share the new proof.
Problem statement
In graph theory, the degree of a vertex

A well-known property is that every undirected graph contains an even number of vertices with odd degree. The result first appeared in Euler’s 1736 paper on the Seven Bridges of Königsberg and is also known as the handshaking lemma (that’s because another way of formulating the property is that the number of people that have shaken hands an odd number of times is even).
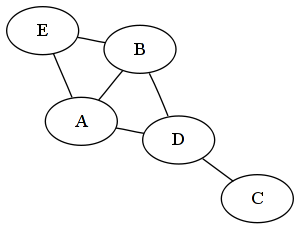
As we can easily verify, the graph shown above satisfies this property. There are four
vertices with odd degree (
Although the proof of this property is simple, all the conventional proofs that I know of are not goal-oriented. My goal is to show you a development of a goal-oriented proof. Also, my proof is completely guided by the shape of the formulae involved, which helps reducing the amount of guessing involved.
Notations that I use
Before we start, let me explain the notations that I use. I assume the
existence of two predicates,
An advantage of using a systematic notation for quantifiers is that we can
write the rules that manipulate quantifiers in a very general way. For example,
suppose that the quantifier
Then, the so-called trading rule is valid:
This rule applies to all quantifiers that generalise operators with units.
For example, because true is the unit of
which is the same as
Calculating a solution to the handshaking lemma
Now, the first step in any goal-oriented solution is to express the goal. In
other words, what do we want to prove or calculate? Using the notation just
described and assuming that the variable
Note that we are adding 1 (counting) for each vertex
We know that the predicate
This calculation shows that the parity of the number of vertices with odd degree is the same as the parity of the sum of all the degrees. But because each edge has two ends, the sum of all the degrees is simply twice the total number of edges. We thus have:
And so we can conclude that every undirected graph contains an even number of vertices with odd degree.
What is wrong with conventional solutions? Conventional solutions for this problem are usually very similar to the following one, taken from the book “Ingenuity in Mathematics” (p. 8), by Ross Honsberger:
The proof in general is simple. We denote by T the total of all the local degrees:
(1) T = d(A) + d(B) + d(C) + … + d(K) .
In evaluating T we count the number of edges running into A, the number into B, etc., and add. Because each edge has two ends, T is simply twice the number of edges; hence T is even.
Now the values d(P) on the right-hand side of (1) which are even add up to a sub-total which is also even. The remaining values d(P) each of which is odd, must also add up to an even sub-total (since T is even). This shows that there is an even number of odd d(P)’s (it takes an even number of odd numbers to give an even sum). Thus there must be an even number of vertices with odd local degree.
There is nothing wrong with this solution in the sense that it shows why the property holds. However, it is clearly oriented to verification: it starts by introducing the total sum of all the local degrees, observing that its value is even; then it analyses that sum to conclude the property. The question is: how can we teach students to come with the total sum of all the local degrees? In general, how can we teach students to come with seemingly unrelated concepts that will be crucial in the development of their arguments? I don’t think we can.
On the other hand, if we look at the goal-oriented proof, we see that the goal is simple to express. Furthermore, with some training, most students would write it correctly and would be able to calculate that the parity of the number of vertices with odd degree is the same as the parity of the sum of all the degrees. And then (and only then) the introduction of the total sum of all the degrees would make sense. In a way, goal-oriented calculations are like that famous masked magician that reveals magic’s biggest secrets, for they reveal how the rabbit got into the hat.