A Square Grid Path Problem

Last November I solved Problem 15 of Project Euler (a counting problem involving paths in square grids), and, although the problem admits a simple solution, some of the solutions presented in their forums are very complicated. Thus, I thought it would be a good idea to present my solution, as I consider it very simple.

Problem statement

Starting in the top left corner of a $2{\times}2$ grid, there are 6 routes (without backtracking) to the bottom right corner.

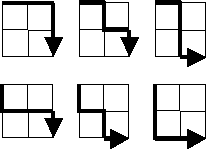
How many routes are there through a 20×20 grid?

My solution

In order to make the problem more interesting, let us investigate the more general problem of counting the number of routes in an $n{\times}n$ grid. Our argument is based on three observations:

1. all the paths have size $2{\times}n$ (the reason is obvious: you have to go right $n$ positions and down another $n$ positions);

2. since we can only go right or down, we can identify every path by a string of Rs and Ds, where an R means going right and a D means going down; as an example, the paths illustrated in the problem statement are (from left to right and from top to bottom): RRDD, RDRD, RDDR, DRRD, DRDR and DDRR;

3. the strings mentioned above must contain the same number of Rs and Ds.

From these three observations, we can transform the problem to the following:

How many different strings of size $2{\times}n$, consisting of n Rs and n Ds, are there?

The solution is now very simple, because the positioning of $n$ Ds (or Rs) determines the positioning of the other $n$ Rs (or Ds). Hence, the number we are interested in is the number of ways in which we can choose $n$ positions from $2{\times}n$ available positions. The answer, using the traditional notation for the binomial coefficient, is:

$${2n \choose n} = \frac{(2n)!}{n! \times n!}~~~~.$$

Instantiating $n$ with 20, we get the answer to the initial problem of the $20{\times}20$ grid.

Generalization to $m{\times}n$ grids

The generalization to an $m{\times}n$ grid is also simple. The only difference is that the strings have length $m+n$. Using the same reasoning as above, the number of paths through an $m{\times}n$ grid is:

$${m+n \choose n} = \frac{(m+n)!}{m!\times n!}~~~~.$$

Final note: If you want to access the forum of the problem, you have to solve it.